07-梯度消失和梯度爆炸的原因及解决方法

问题

梯度消失无论是笔试还是面试都是常客了，其实对应于梯度消失，还有一个梯度爆炸的概念，这又是什么导致的呢？下面我们将根据公式推导来解释何为梯度消失与梯度爆炸。

梯度消失和梯度爆炸的表现

网络层数越多，模型训练的时候便越容易出现 梯度消失(gradient vanish) 和 梯度爆炸(gradient explod) 这种梯度不稳定的问题。假设现在有一个含有３层隐含层的神经网络：

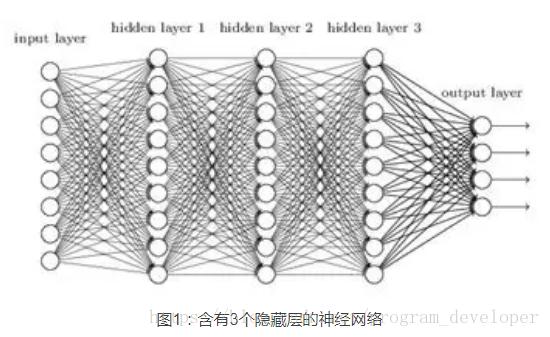
梯度消失发生时的表现是：靠近输出层的 hidden layer 3 的权值更新正常，但是靠近输入层的 hidden layer 1 的权值更新非常慢，导致其权值几乎不变，仍接近于初始化的权值。这就导致 hidden layer 1 相当于只是一个映射层，对所有的输入做了一个函数映射，这时的深度学习网络的学习等价于只有后几层的隐含层网络在学习。

梯度爆炸发生时的表现是：当初始的权值太大，靠近输入层的 hidden layer 1 的权值变化比靠近输出层的 hidden layer 3 的权值变化更快。

所以梯度消失和梯度爆炸都是出现在靠近输入层的参数中。

产生梯度消失与梯度爆炸的根本原因

梯度消失分析

下图是我画的一个非常简单的神经网络，每层都只有一个神经元，且神经元所用的激活函数 $\sigma$ 为 sigmoid 函数，$Loss$ 表示损失函数，前一层的输出与后一层的输入关系如下：
$$
y_i = \sigma(z_i) = \sigma(w_i*x_i+b_i), \quad其中x_i = y_{i-1}
$$

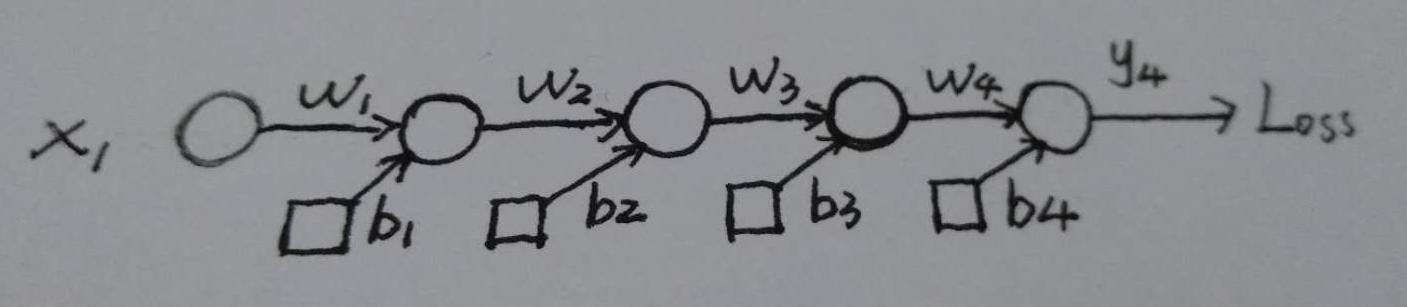
因此，根据反向传播的链式法则，损失函数相对于参数 $b_1$ 的梯度计算公式如下：
$$
\frac{\partial Loss}{\partial b_1} = \frac{\partial Loss}{\partial y_4}*\frac{\partial y_4}{\partial z_4}*\frac{\partial z_4}{\partial x_4}*\frac{\partial x_4}{\partial z_3}*\frac{\partial z_3}{\partial x_3}*\frac{\partial x_3}{\partial z_2}*\frac{\partial z_2}{\partial x_2}*\frac{\partial x_2}{\partial z_1}*\frac{\partial z_1}{\partial b_1} \
= \frac{\partial Loss}{\partial y_4}*\partial{‘}(z_4)w_4\partial{‘}(z_3)w_3\partial{‘}(z_2)w_2\partial{‘}(z_1)
$$
而 sigmoid 函数的导数 $\sigma{‘}(x)$ 如下图所示：

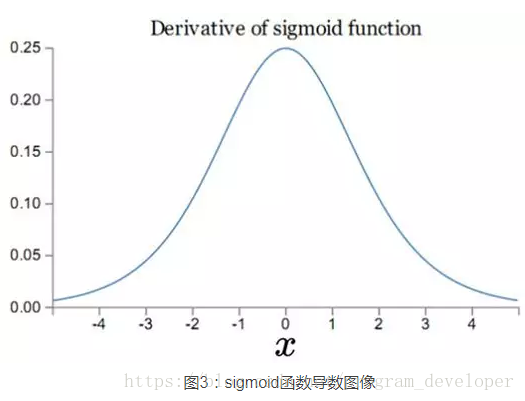
即 $\sigma{‘}(x)\le \frac{1}{4}$ ，而我们一般会使用标准方法来初始化网络权重，即使用一个均值为 0 标准差为 1 的高斯分布，因此初始化的网络参数 $w_i$ 通常都小于 1 ，从而有 $|\sigma{‘}(z_i)w_i|\le \frac{1}{4}$ 。*根据公式(2)的计算规律，层数越多，越是前面的层的参数的求导结果越小，于是便导致了梯度消失情况的出现。

梯度爆炸分析

在分析梯度消失时，我们明白了导致其发生的主要原因是　$|\sigma{‘}(z_i)*w_i|\le \frac{1}{4}$ ，经链式法则反向传播后，越靠近输入层的参数的梯度越小。而导致梯度爆炸的原因是：$|\sigma{‘}(z_i)*w_i|>1$，当该表达式大于 1 时，经链式法则的指数倍传播后，前面层的参数的梯度会非常大，从而出现梯度爆炸。

但是要使得$|\sigma{‘}(z_i)w_i|>1$，就得 $|w_i| > 4$才行，按照 $|\sigma{‘}(w_ix_i+b_i)w_i|>1$，可以计算出 $x_i$ 的数值变化范围很窄，仅在公式(3)的范围内，才会出现梯度爆炸，*因此梯度爆炸问题在使用 sigmoid 激活函数时出现的情况较少，不容易发生。

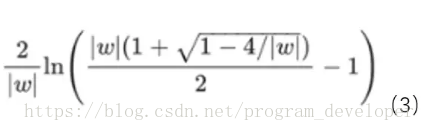
怎么解决

如上分析，造成梯度消失和梯度爆炸问题是网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。另外一个原因是当激活函数使用 sigmoid 时，梯度消失问题更容易发生，因此可以考虑的解决方法如下：

1. 压缩模型层数
2. 改用其他的激活函数如 ReLU
3. 使用 BN 层
4. 使用 ResNet 的短路连接结构(没有解决爆炸问题)

参考资料

激活函数及其作用以及梯度消失、爆炸、神经元节点死亡的解释