08-softmax函数求导过程

问题

今天小伙伴问会不会梯度求导，发现自己对离散变量求导并不熟悉，所以以somafmax为例子复习下，再进阶其实了解计算图了。

softmax函数

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组$Z$，$Z_i$表示$Z$中的第i个元素，那么这个元素的softmax值就是:

​ $$S_i = \frac {e^{z_i}}{\sum_{j}e^{z_j}}$$

更形象的如下图表示：

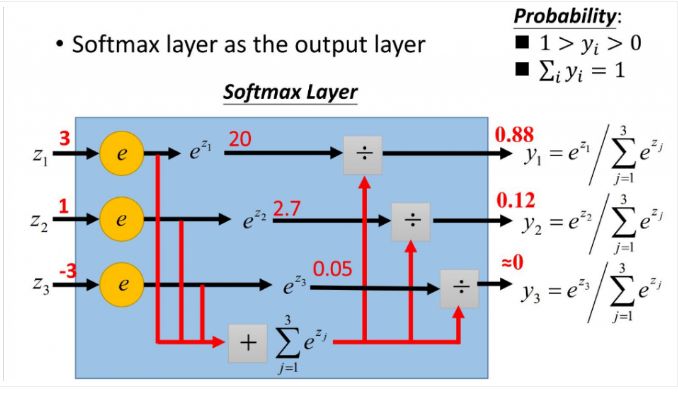
softmax直白来说就是将原来输出是3,1,-3 通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

softmax求导

在神经网络中，我们经常可以看到以下公式，用于计算结点的激活值：

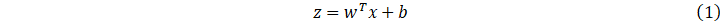
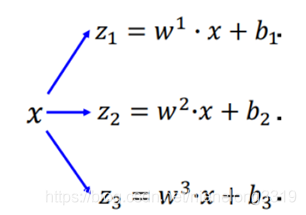
计算示意图如下：

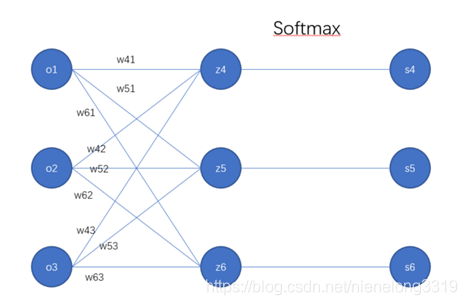
从图中可以得到:

$z4 = w41o1+w42o2+w43*o3 + b14$

$z5 = w51o1+w52o2+w53*o3 + b25$

$z6 = w61o1+w62o2+w63*o3 + b36$

直接甩出Softmax的公式：

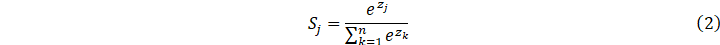
表示类别数，z表示输出向量，zj表示向量z的第j个值。

对Softmax求导：显然是目标是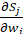和

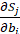
根据求导的链式法则：

所以核心问题就转换为求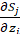 ，在接触到这个式子的时候，考虑到一个问题，为什么这里是对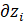求导而不是对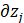求导，因为要考虑

$i = j 和 i != j$的情况。

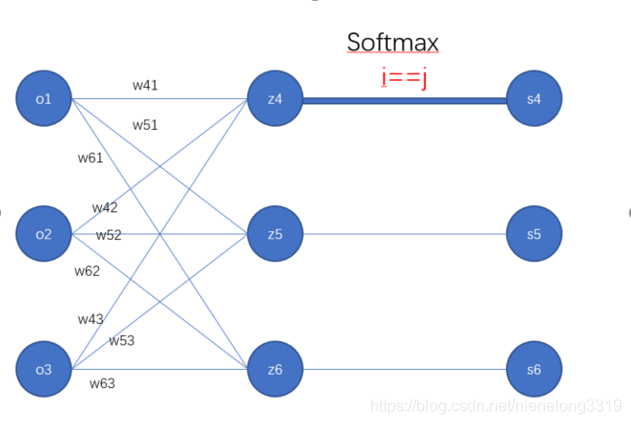
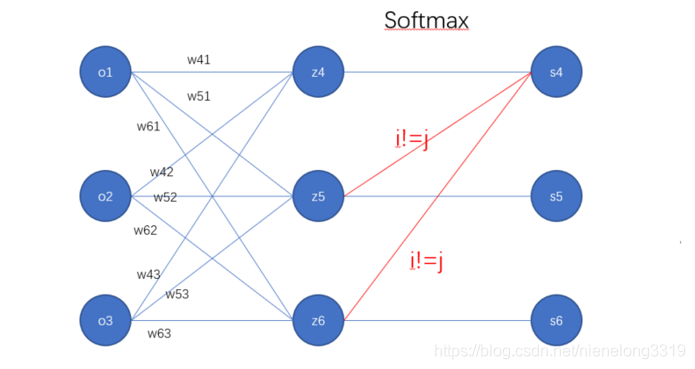
到此我们就能求出w和b了的梯度用于参数更新了，注意输入x维度(3,1), w维度(3,3), b维度(3,1),

$w_{41}$的梯度是怎么计算的了，根据上面的图路线是：$s_4->z_4->o_1$, 此时i=j, 由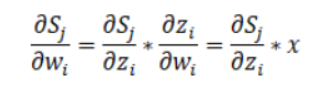，可得$s_4(1-s_4)*o1$, 其他以此内推。

torch实现

import torch
import numpy as np
# 设置随机值
def seed_set(seed):
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    #torch.cuda.manual_seed_all(seed)  # if you are using multi-GPU.
    torch.backends.cudnn.deterministic = True
    torch.backends.cudnn.benchmark = False

seed_set(42)

w = torch.rand((4, 10))
a = torch.rand((10, 10), requires_grad=True)


b = a.sum(dim=0, keepdim=True)
c = a/b
y = w@c

vals = list(globals().values())
for xx in vals:
  if isinstance(xx, torch.Tensor):
    if xx.requires_grad: xx.retain_grad()

torch.sum(y).backward()
print(y.grad)
print(c.grad)
print(b.grad)
print(a.grad)

exit()

参考

详解softmax函数以及相关求导过程

softmax 函数以及相关求导过程+交叉熵