14-卷积与互相关的联系

卷积层的来源与作用

深度学习的计算机视觉是基于卷积神经网络实现的，卷积神经网络的与传统的神经网络（可以理解为多层感知机）的主要区别是卷积神经网络中除了全连接层外还有卷积层和pooling层等。

卷积层算是图像处理中非常基础的东西，它其实也是全连接层演变来的，卷积可视为局部连接和共享参数的全连接层。

局部连接：在全连接层中，每个输出通过权值(weight)和所有输入相连。而在视觉识别中，关键性的图像特征、边缘、角点等只占据了整张图像的一小部分，图像中相距很远的两个像素之间有相互影响的可能性很小。因此，**在卷积层中，每个输出神经元在通道方向保持全连接，而在空间方向上只和一小部分输入神经元相连。**

共享参数： 使用同一组权值去遍历整张图像，用于发现整张图像中的同一种特征例如角点、边缘等。不同的卷积核用于发现不同的特征。共享参数是深度学习一个重要的思想，其在减少网络参数的同时仍然能保持很高的网络容量(capacity)。卷积层在空间方向共享参数，而循环神经网络(recurrent neural networks)在时间方向共享参数。

卷积层的作用：通过卷积，我们可以捕获图像的局部信息。通过多层卷积层堆叠，各层提取到特征逐渐由边缘、纹理、方向等低层级特征过度到文字、车轮、人脸等高层级特征。

卷积与互相关

但是其实深度学习各框架的conv2卷积层的API对卷积运算的实现其实使用的是互相关运算，即下图：

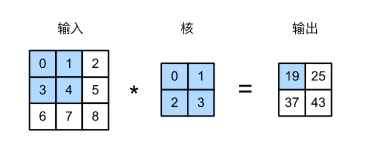
在这里插入图片描述

上述的运算过程可以写成公式：

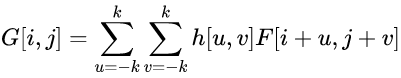
在这里插入图片描述

h[u, v]表示filter的权重；k表示neighbor的个数，如当k=1时表示的是3*3的滤波器

从公式中可以看出这个运算是从上往下，从左到右的对点相乘再相加。所以这个公式代表的运算是互相关。

下面我们回顾下卷积的定义，设f(x)和g(x)是在R上的可积函数，作积分：

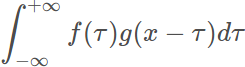
在这里插入图片描述

改成离散函数形式如下：

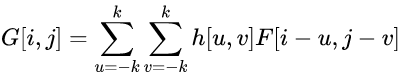
在这里插入图片描述

这个公式与互相关的公式很相似，但是注意符号改变了，这就导致运算的方向变成了从下往上，从右到左，与互相关的运算顺序刚好相反。

所以真正的卷积运算应该是先让卷积核绕自己的核心元素顺时针旋转180度（或者理解为左右翻转再上下翻转），再与图像中的像素做对点相乘再相加运算。

然而图像处理中的大部分卷积核都是中心对称的，所以这时候的互相关运算与卷积运算结果是一样的，这也许是最开始称为卷积的原因吧。

另外CNN中的卷积核权值参数是学出来的，所以其实卷积和互相关没啥区别

将卷积运算转为矩阵相乘

这里先扯一扯之前没怎么听过但突然看到的量化概念。

传统优化矩阵乘的思想有基于算法分析的，也有基于软件优化的方法如改进访存局部性、利用向量指令等，这两个方法都是基于对计算机运行特性进行的改进。

而随着深度学习技术的演进，神经网络技术出现了一个重要的方向——神经网络量化，。量化技术的出现使得我们可以在深度学习领域使用一些特别的方法来优化矩阵乘，例如facebook开源的专门用于量化神经网络的计算加速库QNNPACK。

神经网络计算一般都是以单精度浮点(Floating-point 32, FP32)为基础。而网络算法的发展使得神经网络对计算和内存的要求越来越大，以至于移动设备根本无力承受。为了提升计算速度，量化(Quantization)被引入到神经网络中，主流的方法是将神经网络算法中的权重参数和计算都从FP32转换到INT8。这里有个相关的论文：CVPR2020 | 8 比特数值也能训练模型？商汤提出训练加速新算法（反正我是看不明白，就是提提相关概念）

下面讲解传统的卷积运算怎么转化为矩阵乘：

传统的卷积核依次滑动的计算方法很难加速。转化为矩阵乘法之后，就可以调用各种线性代数运算库，CUDA里面的矩阵乘法实现。这些矩阵乘法都是极限优化过的，比暴力计算快很多倍。下面的两个图充分说明了转化为矩阵乘法后的具体过程：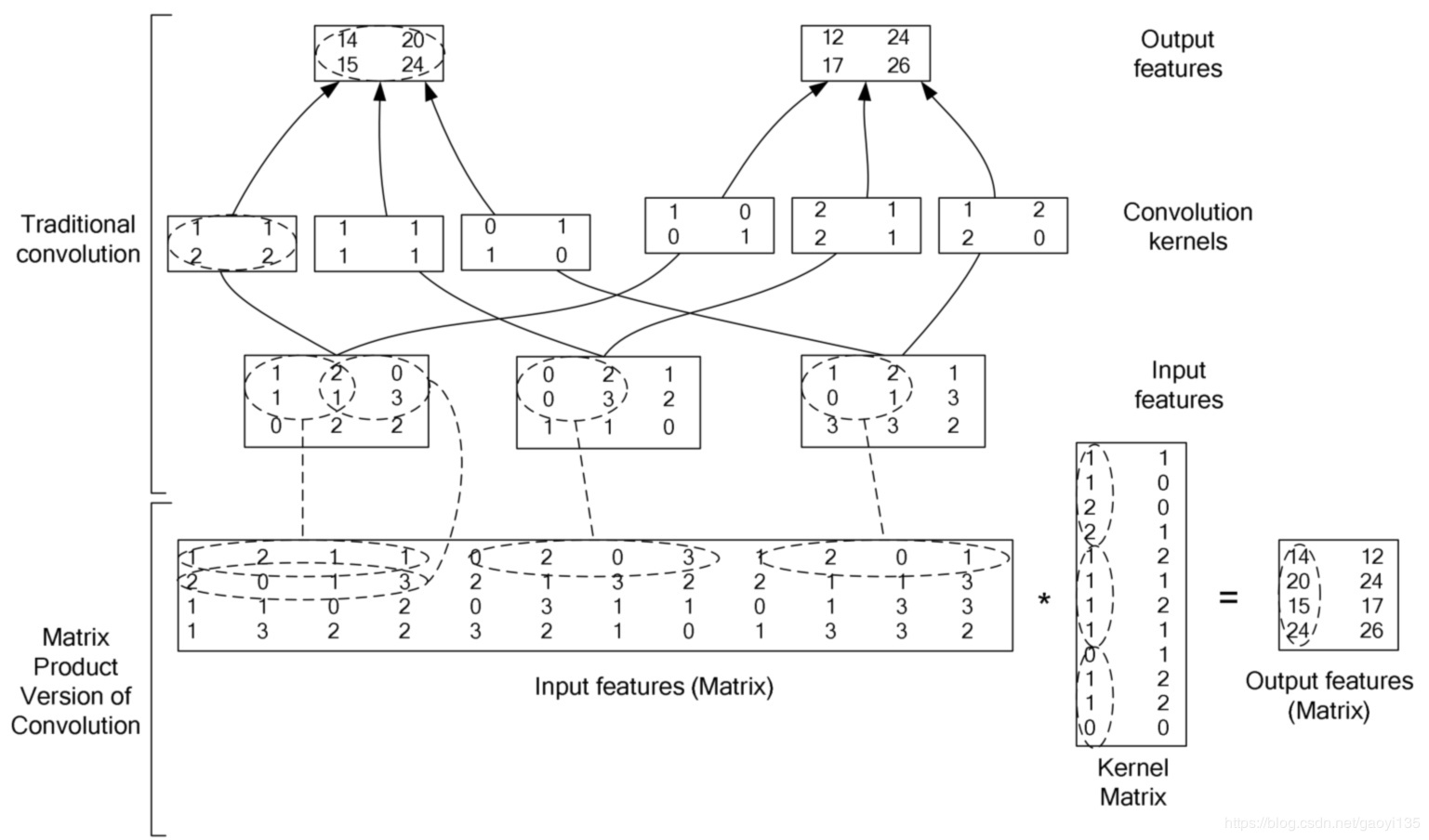
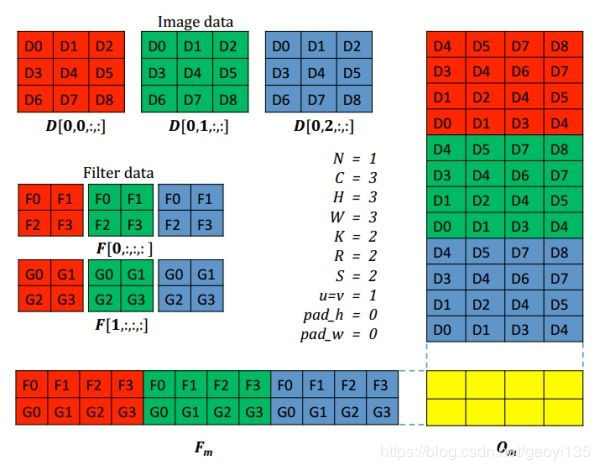
在这里插入图片描述