17-各种卷积操作串讲

问题

CNN 从 2012 年的 AlexNet 发展至今，各种网络结构层出不穷，尝试了几乎所有可能性的结构搭配以试图找到效果更好的那种，再通过结果去解释过程，这大概就是做深度学习的人的无奈之处吧，每天都有新论文发出，每天都会有新的网络结果，每个都比之前的提升一丢丢，琳琅满目，令人眼花缭乱，像我这样的便迷失其中，找不到一个确定的方向去研究，终究普普通通，无所建树。

网络结构如此，卷积 (Convolution) 方式也不例外，各种可能性的卷积过程改变方式都出现了（以后大概还有出现新的卷积方式的），效果各异，特点不同，所以想通过这篇文章将各种卷积方式捋一捋，体会下大牛们的智慧！

符号约定

输入：$H_{in}*W_{in}*C_{in}$ ，其中 $H_{in}$ 为输入 feature map 的高，$W_{in}$ 为宽，$C_{in}$ 为通道数

输出：$H_{out}*W_{out}*C_{out}$ ，其中 $H_{out}$ 为输出 feature map 的高，$W_{out}$ 为宽，$C_{out}$ 为通道数

卷积核：$NKK*C_k$ ，其中 $N$ 为该卷积层的卷积核个数，$K$ 为卷积核宽与高(默认相等)，$C_k$ 为卷积核通道数

这里我们先不考虑卷积步长 stride 和 padding 等，这些只影响输入 feature map 的大小。且假定你已熟悉普通意义下的卷积操作。

一、常规卷积(Convolution)

特点：

1. 卷积核通道数与输入 feature map 的通道数相等，即 $C_{in} = C_k$
2. 输出 feature map 的通道数等于卷积核的个数，即 $C_{out} = N$

卷积过程：

卷积核在输入 feature map 中移动，按位点乘后求和即可，卷积的实现过程参考之前写过的一篇文章(03_代码实现卷及操作)。

下面是一个卷积动图，帮助你理解。

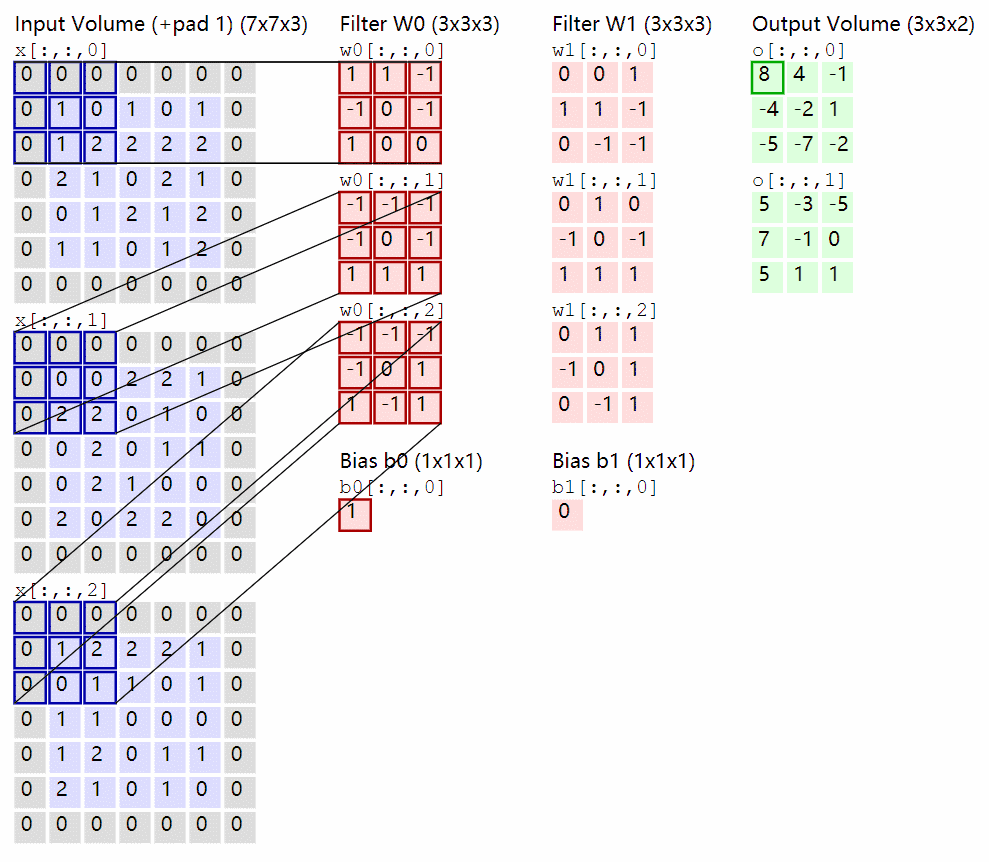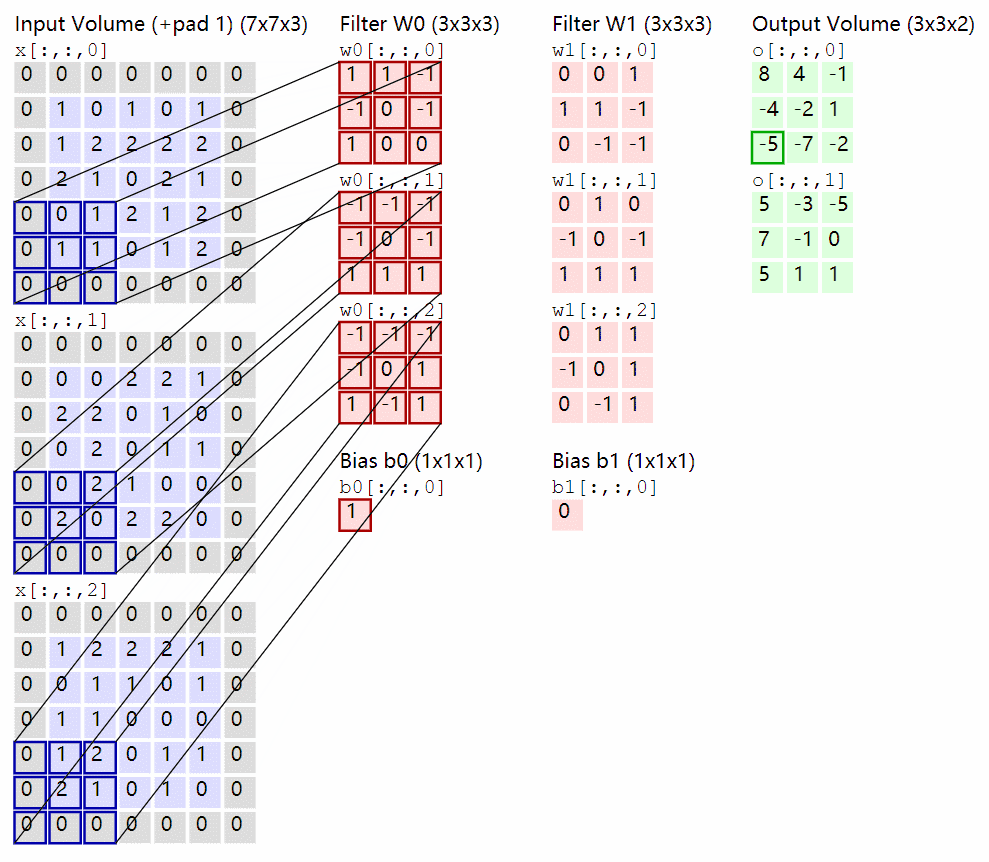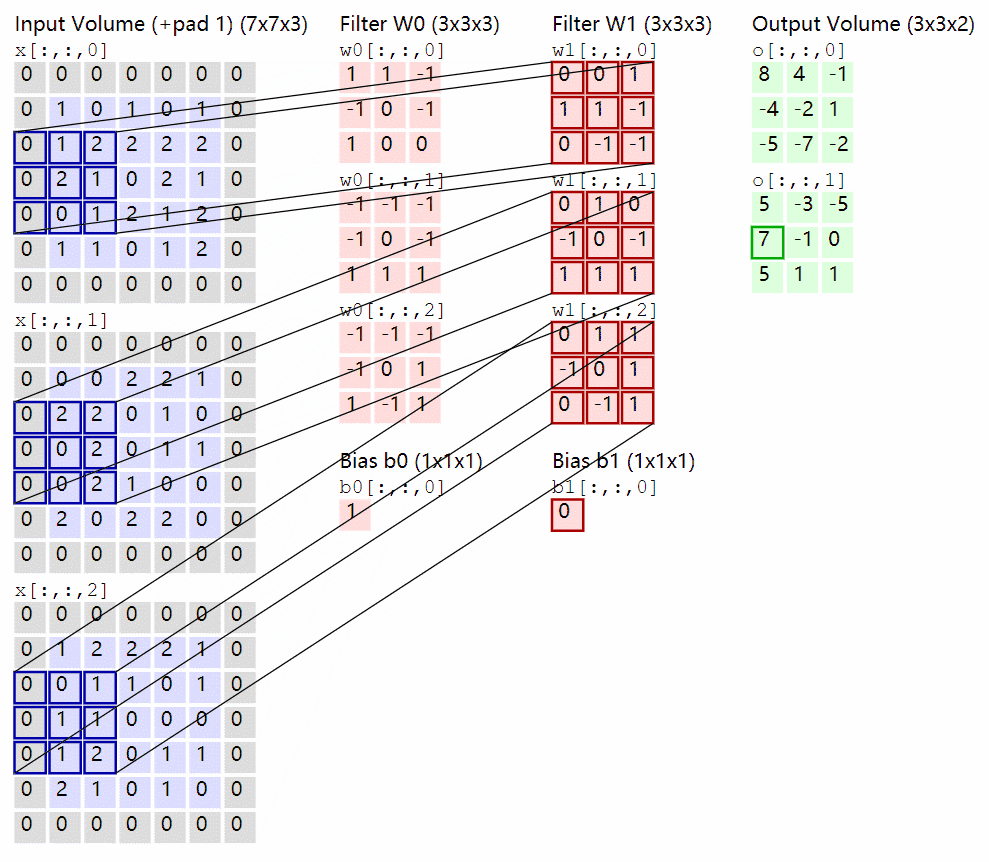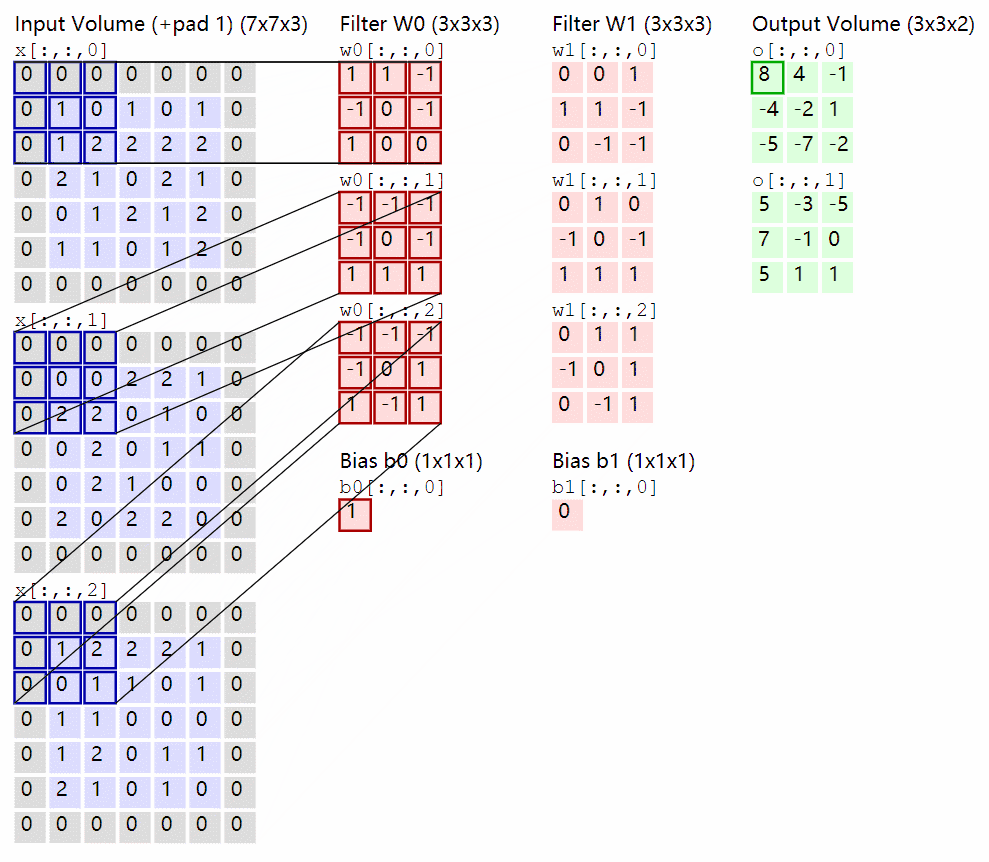
二、1ｘ1卷积

特点：

1. 顾名思义，卷积核大小为 1ｘ1
2. 卷积核通道数与输入 feature map 的通道数相等，即 $C_{in} = C_k$
3. 输出 feature map 的通道数等于卷积核的个数，即 $C_{out} = N$
4. 不改变 feature map 的大小，目的是为了改变 channel 数，即 1ｘ1 卷积的使用场景是：不想改变输入 feature map 的宽高，但想改变它的通道数。即可以用于升维或降维。
5. 相比 3ｘ3 等卷积，计算量及参数量都更小，计算量和参数量的计算参考另一篇文章 (22_CNN网络各种层的FLOPs和参数量paras计算)

作用：

1. 升维或降维。改变 feature map 的大小，目的是为了改变 channel 数，即 1ｘ1 卷积的使用场景是：不想改变输入 feature map 的宽高，但想改变它的通道数
2. 加入非线性。1*1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep。
3. 跨通道信息交互（channal 的变换）。实现降维和升维的操作其实就是channel间信息的线性组合变化

示意图：

(图来自这个博客)

1x1核的主要目的是应用非线性。在神经网络的每一层之后，我们都可以应用一个激活层。无论是ReLU、PReLU、Sigmoid还是其他，与卷积层不同，激活层是非线性的。非线性层扩展了模型的可能性，这也是通常使“深度”网络优于“宽”网络的原因。为了在不显著增加参数和计算量的情况下增加非线性层的数量，我们可以应用一个1x1内核并在它之后添加一个激活层。这有助于给网络增加一层深度。

三、分组卷积(Group convolution)

Group convolution 分组卷积，最早在 AlexNet 中出现，由于当时的硬件资源有限，训练 AlexNet 时卷积操作不能全部放在同一个 GPU 处理，因此作者把 feature maps 分给多个GPU分别进行处理，最后把多个 GPU 的结果进行融合。

卷积过程：

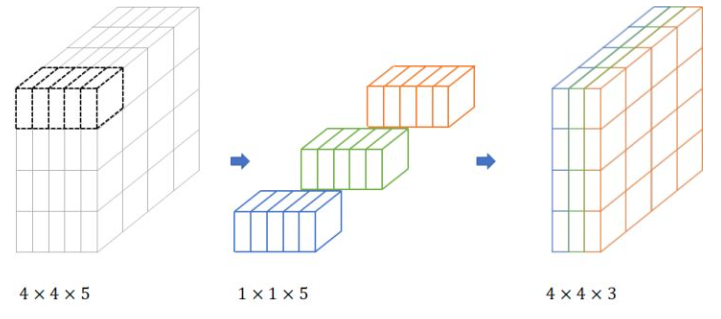
将输入 feature map 分成 g 组，一个卷积核也相对应地分成 g 组，在对应的组内做卷积。（我们可以理解成分组卷积中使用的 g 组卷积核整体对应于常规卷积中的一个卷积核，只不过是将常规卷积中的一个卷积核分成了 g 组而已）

(图来自这个博客)

特点、作用：

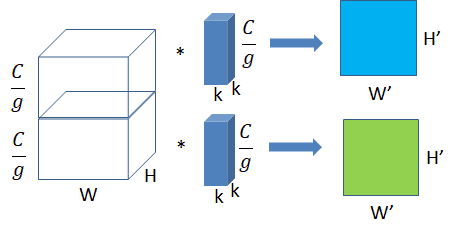
1. 输入的 feature map 尺寸：$H_{in}W_{in} \frac{C_{in}}{g}$ ，共有 g 组
2. 卷积核的规格：$NKK*\frac{C_{k}}{g}$，共有 N * g 组
3. 输出 feature map 规格：$H_{out}W_{out}Ng$ ，共生成 Ng 个 feature map
4. 当 $g = 1$ 时就退化成了上面讲过的常规卷积，当 $g = C_{in}$ 时就是我们下面将要讲述的深度分离卷积。
5. 用常规卷积得到一个输出 feature map 的计算量和参数量便可以得到 g 个输出 feature map，所以分组卷积常用在轻量型高效网络中，因为它可以用少量的参数量和计算量生成大量的 feature map。

四、可分离卷积

可分离卷积又分成两种：空间可分离卷积 和 深度可分离卷积。

空间可分离卷积

之所以命名为空间可分离卷积，是因为它主要处理的是卷积核的空间维度：宽度和高度。

空间可分离卷积简单地将卷积核划分为两个较小的卷积核。 最常见的情况是将3x3的卷积核划分为3x1和1x3的卷积核，如下所示：

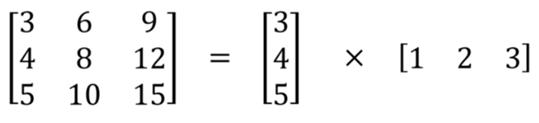
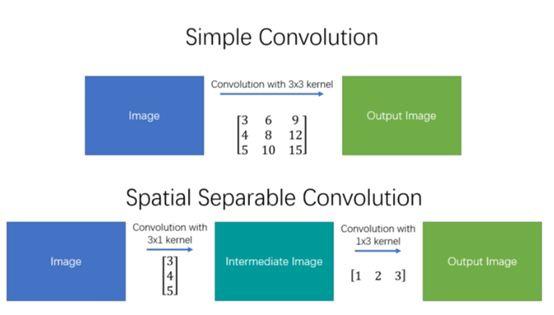
特点：

1. 局限性：并不是所有的卷积核都可以“分离”成两个较小的卷积核，能够“分离”的是那些卷积核参数大小的行和列有一定倍数关系的. 这在训练期间变得特别麻烦，因为网络可能采用所有可能的卷积核，它最终只能使用可以分成两个较小卷积核的一小部分。所以实际中用的不多
2. 参数量和计算量更少：如上图所示，不是用9次乘法进行一次卷积，而是进行两次卷积，每次3次乘法（总共6次），以达到相同的效果。 乘法较少，计算复杂性下降，网络运行速度更快。

深度可分离卷积

与空间可分离卷积不同，深度可分离卷积与卷积核无法“分解”成两个较小的内核。 因此，它更常用。 这是在keras.layers.SeparableConv2D或tf.layers.separable_conv2d中看到的可分离卷积的类型。

之所以命名为深度可分离卷积，是因为第一步卷积的时候是通道独立的（后面会看到这种卷积方式分成两步），你可以将每个通道想象成对该图像特定的解释说明（interpret）; 例如RGB图像中，“R”通道解释每个像素的“红色”，“B”通道解释每个像素的“蓝色”，“G”通道解释每个像素的“绿色”。 有多少个通道就有多少种解释。

卷积过程：

深度可分离卷积的过程分为两部分：深度卷积(depthwise convolution) 和 逐点卷积(pointwise convolution)

(1) 深度卷积

深度卷积意在保持输入 feature map 的通道数，即对 feature map 中的每个通道使用一个规格为 $KK1$ 的卷积核进行卷积，于是输入 feature map 有多少个通道就有多少个这样的卷积核，深度卷积结束后得到的输出的通道数与输入的相等。

这一步其实就相当于常规卷积中的一个卷积核，只不过不同通道的卷积结果不相加而已，自己体会体会。

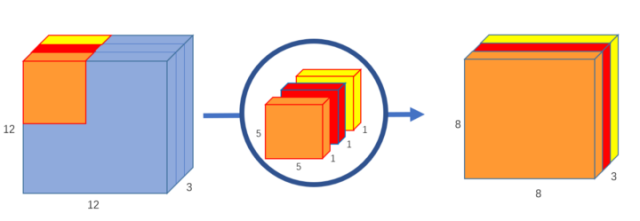
(2) 逐点卷积

在上一步的基础上，运用 1ｘ1 卷积进行逐点卷积。

使用一个 1ｘ1 卷积核就可以得到输出 feature map 一维的结果。

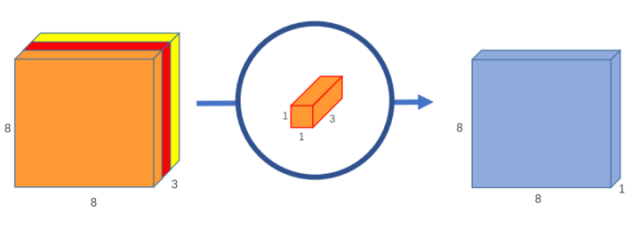
如果你要输出 feature map 有 256 维，那么就使用 256 个 1ｘ1 卷积核即可。

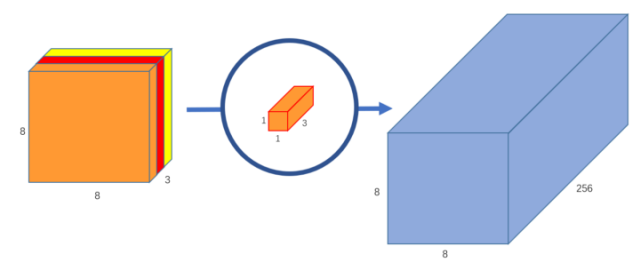
特点：

1. 可以理解成常规的卷积分成了两步执行，但是分成两步后参数量和计算量大大减少，网络运行更快

转置卷积 (transposed convolution)

转置卷积常常用于 CNN 中对特征图进行上采样，比如语义分割和超分辨率任务中。之所以叫转置卷积是因为，它其实是把我们平时所用普通卷积操作中的卷积核做一个转置，然后把普通卷积的输出作为转置卷积的输入，而转置卷积的输出，就是普通卷积的输入。这样说可能有点绕，我们可以参照CNN中的反向传播过程来理解，转置卷积形式上就和一个卷积层的反向梯度计算相同。既然是输入输出对调，那么就有两个很重要的特性：

1. 转置的卷积核变为了普通卷积核的转置
2. 如果把由输入特征图到输出特征图的计算过程画成一个计算图，那么输入输出元素的连接关系是不变的.也就是说，在普通卷积中，若元素a和元素1有连接（元素1由a计算得到），那么在相应的转置卷积中，元素1和元素a依然是有连接的（元素a由元素1计算得到）。

下面通过对比常规卷积和转置卷积的计算过程帮助理解：

常规卷积：

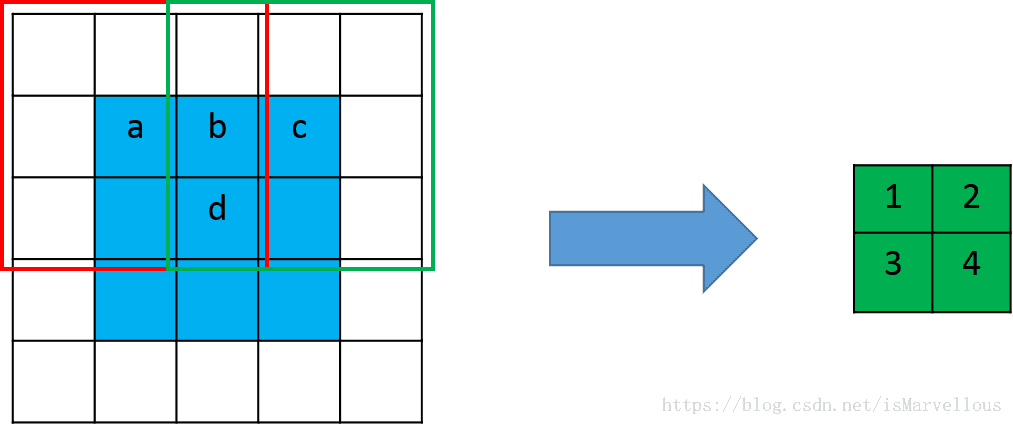
这是一个卷积核大小为3x3，步长为2，padding为1的普通卷积。卷积核在红框位置时输出元素1，在绿色位置时输出元素2。我们可以发现，输入元素a仅和一个输出元素有运算关系，也就是元素1，而输入元素b和输出元素1, 2均有关系。同理c只和一个元素2有关，而d和1,2,3,4四个元素都有关。那么在进行转置卷积时，依然应该保持这个连接关系不变。

转置卷积：

根据前面的分析，我们需要将上图中绿色的特征图作为输入，蓝色的特征图作为输出，并且保证连接关系不变。也就是说，a只和1有关，b和1,2两个元素有关，其它类推。怎么才能达到这个效果呢？我们可以先用0给绿色特征图做插值，插值的个数就是使相邻两个绿色元素的间隔为卷积的步长，同时边缘也需要进行与插值数量相等的补0。如下图：

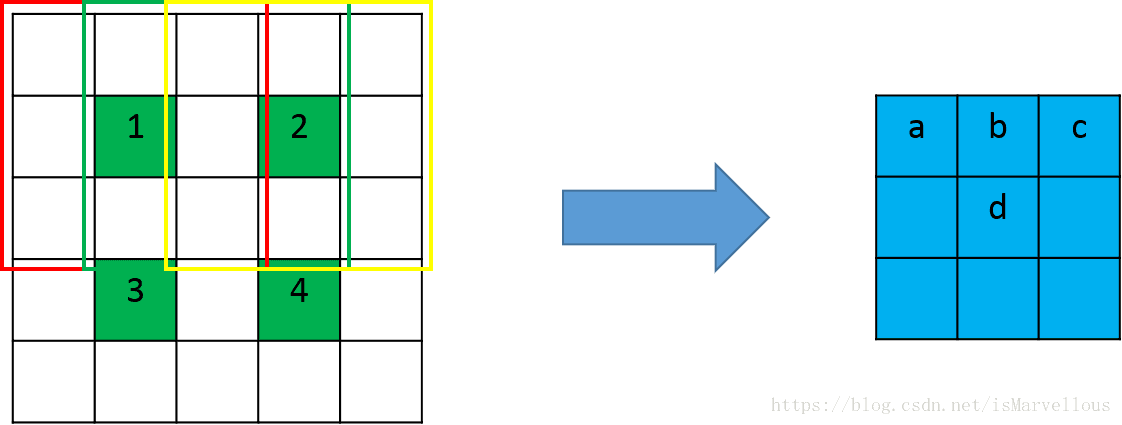
注意，这时候卷积核的滑动步长就不是2了，而是1，步长体现在了插值补0的过程中。

输出特征图的尺寸计算：

假设我们做转置卷积的输入特征图大小为 $nn$，卷积核大小为 $kk$，后面为了表示方便，我们直接使用边长来表示大小。步长stride为 s（注意这个步长是前面做卷积的时候的步长，设计网络结构的时候对应过来即可），那么转置卷积需要在四周每个边缘补0的数量为 s-1，边缘和内部插空补0后输入特征图大小变为：
$$
0插值后的输入特征图大小：sn+s-1
$$
使用大小为 k 的卷积核进行卷积（滑动步长为1），得到的输出特征图大小为：
$$
\frac{sn+s-1-k}{1}+1 = s*n+(s-k)
$$
当然这个公式只是转置卷积的一种理解方法，在实际的实现中，还有不同的padding, stride和dilation配置，输出图像大小也会随之改变。

可能疑惑的地方：

1. 为什么人们很喜欢叫转置卷积为反卷积或逆卷积。首先举一个例子，将一个4x4的输入通过3x3的卷积核在进行普通卷积（无padding, stride=1），将得到一个2x2的输出。而转置卷积将一个2x2的输入通过同样3x3大小的卷积核将得到一个4x4的输出，看起来似乎是普通卷积的逆过程。就好像是加法的逆过程是减法，乘法的逆过程是除法一样，人们自然而然的认为这两个操作似乎是一个可逆的过程。但事实上两者并没有什么关系，操作的过程也不是可逆的。具体对转置卷积名称的理解可参考这篇博客。

转置卷积蛮复杂的，很多博客讲解的角度都不太一样，看得有点晕，这里先放一放，后面有心情了再好好研究下……

空洞卷积 (Dilated / Atrous Convolutions)

空洞卷积诞生在图像分割领域，在一般的卷积结构中因为存在 pooling 操作，目的是增大感受野也增加非线性等，但是 pooling 之后特征图的大小减半，而图像分割是 pixelwise 的，因此后续需要 upsamplng 将变小的特征图恢复到原始大小，这里的 upsampling 主要是通过转置卷积完成，但是经过这么多的操作之后会将很多细节丢失，那么空洞卷积就是来解决这个的，既扩大了感受野，又不用 pooling 。

Dilated/Atrous Convolution 或者是 Convolution with holes 从字面上就很好理解，是在标准的 convolution map 里注入空洞，以此来增加感受野。相比原来的正常卷积，空洞多了一个 超参数，称之为 dilation rate 指的是kernel的间隔数量(e.g. 正常的卷积是 dilatation rate 1)。

在VGG网络中就证明了使用小卷积核叠加来取代大卷积核可以起到减少参数同时达到大卷积核同样大小感受野的功效。但是通过叠加小卷积核来扩大感受野只能线性增长，公式为$(kernelSize - 1)*layers+1$,，也就是线性增长，而空洞卷积可以以指数级增长感受野。

先来感受下空洞卷积和常规卷积的不同之处：Dilated Convolution with a 3 x 3 kernel and dilation rate 2

要理解空洞概念和如何操作可以从两个角度去看。

1. 从原图角度，所谓空洞就是在原图上做采样。采样的频率是根据rate参数来设置的，当rate为1时候，就是原图不丢失任何信息采样，此时卷积操作就是标准的卷积操作，当rate>1，比如2的时候，就是在原图上每隔一（rate-1）个像素采样，如图b，可以把红色的点想象成在原图上的采样点，然后将采样后的图像与kernel做卷积，这样做其实变相增大了感受野。
2. 从kernel角度去看空洞的话就是扩大kernel的尺寸，在kernel中，相邻点之间插入rate-1个零，然后将扩大的kernel和原图做卷积 ，这样还是增大了感受野。

在语义分割任务中，当它与双线性插值一起使用时，可以替代转置卷积。

参考资料

卷积网络CNN中各种常见卷积过程
可分离卷积基本介绍
CNN中卷积操作十大改进方向
关于转置卷积（反卷积）的理解
Dilated/Atrous conv 空洞卷积