01—三种常见激活函数

问题

在笔试问答题或面试中偶尔有涉及到激活函数的问题，这里简单总结一下深度学习中常见的三种激活函数sigmoid、tanh和ReLU，以及它们各自的特点和用途。

激活函数

激活函数的作用是什么？

激活函数的主要作用是在神经网络中引入非线性因素。

优秀激活函数具备的特性

非线性
可微基于梯度优化必备特性
单调性 激活函数单调保证单层网络是凸函数，凸函数的局部最优解即为全局最优
计算简单 减少计算资源
非饱和性 饱和区导数近乎为0，易出现梯度消失现象
值域有限，优化稳定些；无限，训练高效，但学习率要小点

常见的三种激活函数

	sigmoid	tanh	ReLU
公式	$f(x)=\frac{1}{1+e^{-x}}$	$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$	$f(x)=max(0,x)$
导数	$f’(x)=f(x)(1-f(x))$	$f’(x)=1-f^2(x)$	$f’(x)=\begin{cases}1,x>0\0,x\leq0\end{cases}$
梯度消失	容易造成	也容易造成，但优于sigmoid	可以减缓，优于前两者
常见应用	二分类任务	RNN网络	CNN网络
优点	函数平滑，容易求导	①函数平滑，容易求导 ②输出关于零点对称	①求导更快，收敛更快 ②有效缓解了梯度消失问题 ③增加网络的稀疏性
缺点	①容易造成梯度消失 ②存在幂运算，计算量大 ③其输出不关于零点对称	①容易造成梯度消失 ②同样存在计算量大的问题	容易造成神经元的“死亡”
图形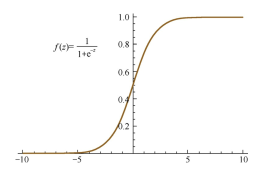

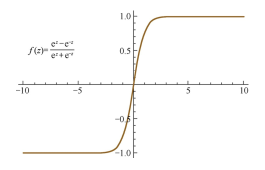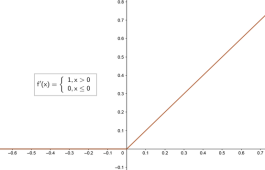拓展

相比于sigmoid函数，tanh激活函数输出关于“零点”对称的好处是什么？

对于sigmoid函数而言，其输出始终为正，这会导致在深度网络训练中模型的收敛速度变慢，因为在反向传播链式求导过程中，权重更新的效率会降低（具体推导可以参考这篇文章）。

此外，sigmoid函数的输出均大于0，作为下层神经元的输入会导致下层输入不是0均值的，随着网络的加深可能会使得原始数据的分布发生改变。而在深度学习的网络训练中，经常需要将数据处理成零均值分布的情况，以提高收敛效率，因此tanh函数更加符合这个要求。

sigmoid函数的输出在[0,1]之间，比较适合用于二分类问题。

为什么RNN中常用tanh函数作为激活函数而不是ReLU？

详细分析可以参考这篇文章。下面简单用自己的话总结一下：

RNN中将tanh函数作为激活函数本身就存在梯度消失的问题，而ReLU本就是为了克服梯度消失问题而生的，那为什么不能直接（注意：这里说的是直接替代，事实上通过截断优化ReLU仍可以在RNN中取得很好的表现）用ReLU来代替RNN中的tanh来作为激活函数呢？这是因为ReLU的导数只能为0或1，而导数为1的时候在RNN中很容易造成梯度爆炸问题。

为什么会出现梯度爆炸的问题呢？因为在RNN中，每个神经元在不同的时刻都共享一个参数W（这点与CNN不同，CNN中每一层都使用独立的参数$W_i$），因此在前向和反向传播中，每个神经元的输出都会作为下一个时刻本神经元的输入，从某种意义上来讲相当于对其参数矩阵W作了连乘，如果W中有其中一个特征值大于1，则多次累乘之后的结果将非常大，自然就产生了梯度爆炸的问题。

那为什么ReLU在CNN中不存在连乘的梯度爆炸问题呢？因为在CNN中，每一层都有不同的参数$W_i$，有的特征值大于1，有的小于1，在某种意义上可以理解为抵消了梯度爆炸的可能。